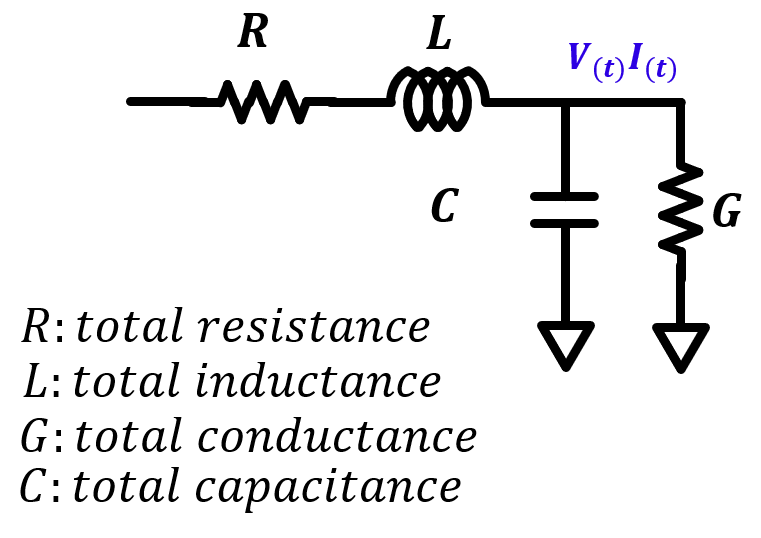
Figure 1 shows approximation of a transmission line with lumped elements. A section of distributed transmission line can be modelled using resistors, capacitors and inductors as shown in the figure. The model approximates distributed circuit operation as we consider the limit \(\Delta x \rightarrow 0\). To derive telegrapher's equation from this model, we can apply ohm's and Kirchoff's law to nodes at location \(x\) and \(x+\Delta x\). Detailed derivation process is shown in the figure below.

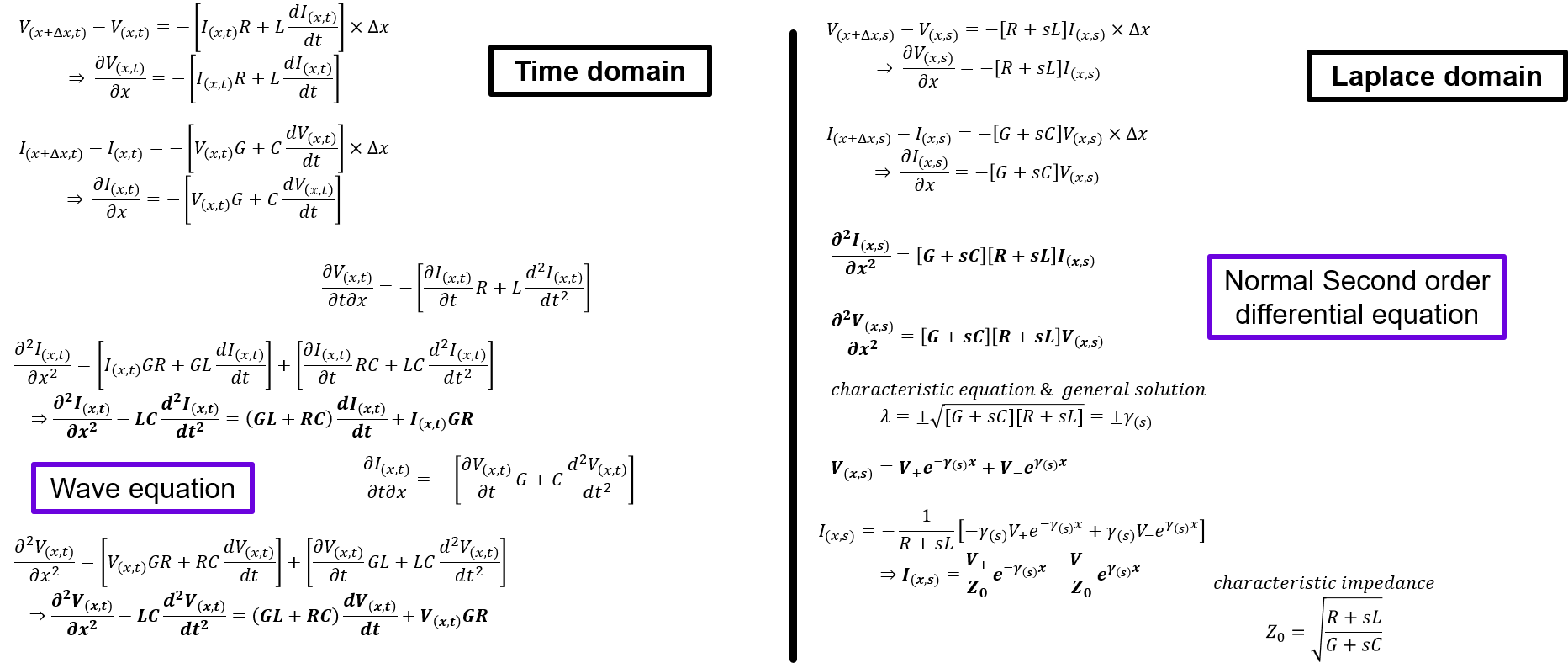
In time-domain derivation, we obtained typical known form of Telegrapher's equation which is in the family of wave equations. This type of equation is well studied and will yield us wave functions as solutions. While time domain derivation is good and all, in Laplace domain, the derivation becomes much simpler and intuitive. The resulting Telegrapher's equation is somewhat reduced to second order differential equation which is much easier to calculate. In the laplace domain solution, we can indeed see that the general solution is two waves going to both ends of the transmission line as shown in FIgure 3 below.

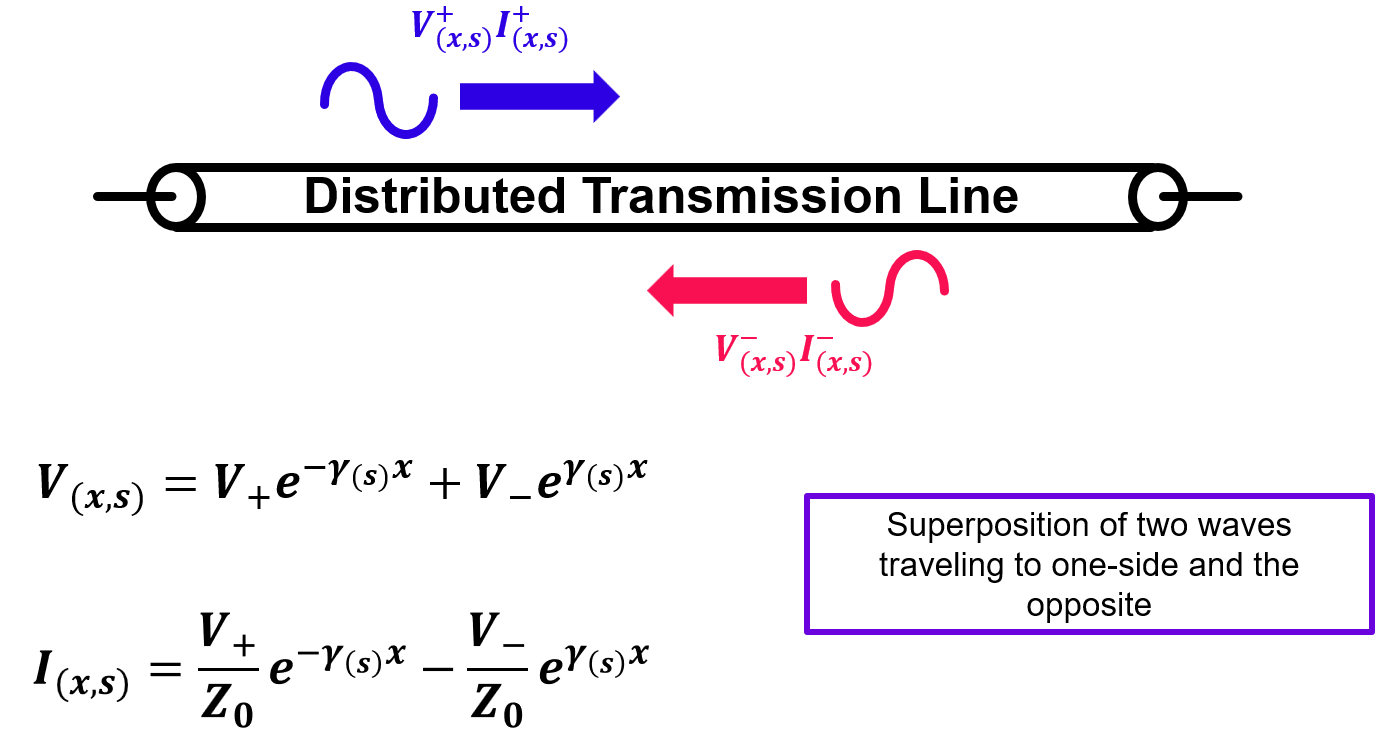
To conclude, in this article we explored Telegrapher's equation derivation in time and Laplace domain. Derivation in Laplace domain is much simpler and yield us more direct insight into the solution, which is superposition of two waves travelling to both ends of the transmission line. In the next chapters we are going to explore several examples which will showcase how intuitive and easy it is to apply the derived laplace domain result in real problems.