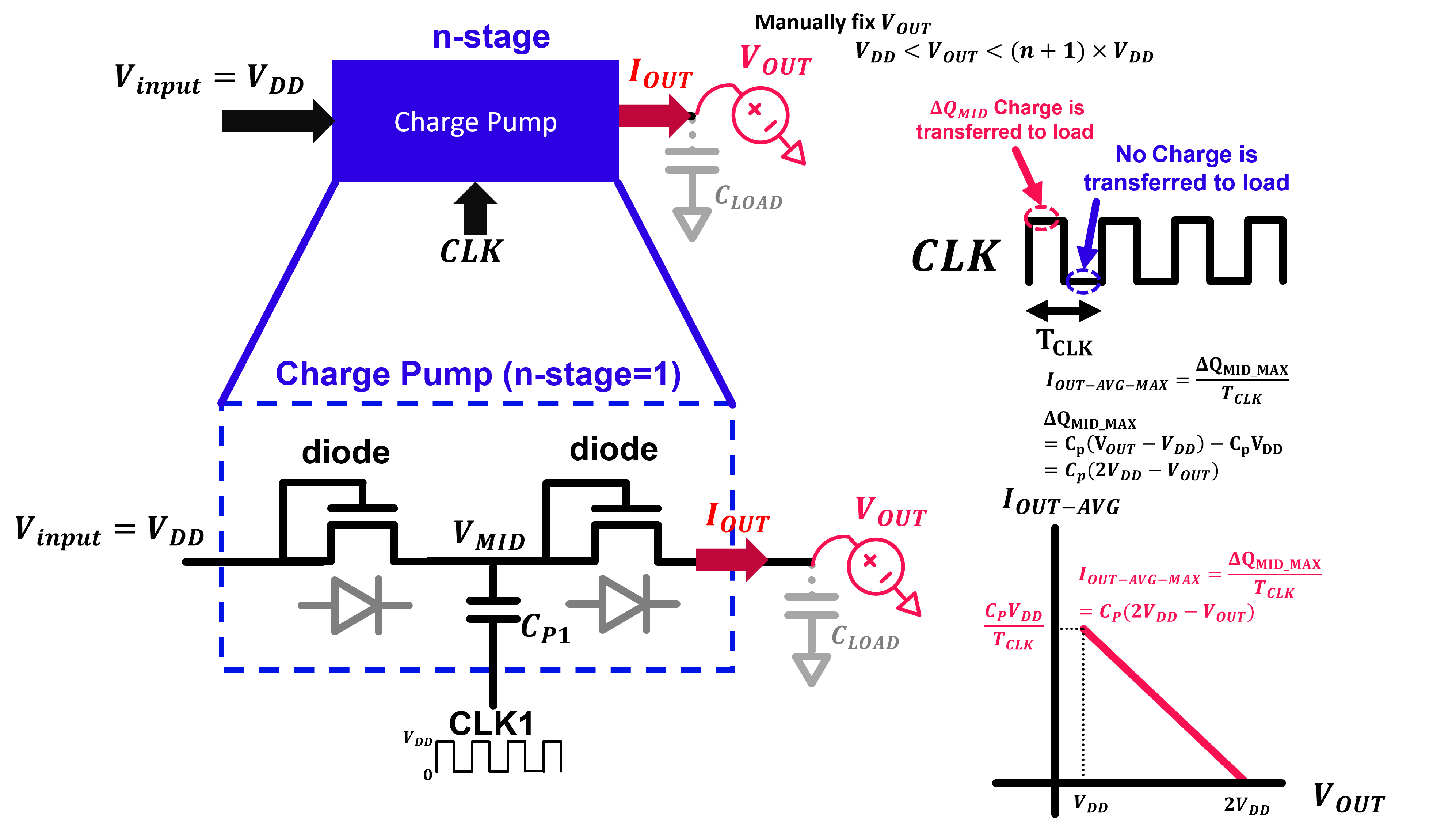
When considering charge pump output current, we usually center our argument around the average current that a charge pump can provide to its load over each clock period. We can obtain the average current of a charge pump by dividing the number of transferred charge with clock period as follows: \[ I_{OUT-AVG}=\frac{\Delta Charge}{T_{CLK}} \] In the previous chapter, we derived that the amount of charge which can be transferred at each clock period is limited to \(\Delta Q_{LOAD}\) . Hence our equations become: \[ I_{OUT-AVG}=\frac{\Delta Q_{LOAD}}{T_{CLK}} \] \[ I_{OUT-AVG}=\frac{( 2V_{DD}-V_{0} )\frac{C_{p}}{C_{p}+C_{LOAD}}}{T_{CLK}} \] From the above equation, we see that the amount of current which can be supplied by a charge pump is dependent on voltage level at its output node. We can plot this quantity with respect to Vout to obtain charge pump current curve as shown in the right side of the figure. \(I_{OUT-AVG}\) is highest when Vout level is low and tends to 0 as Vout approaches 2VDD.

To observe charge pump current behavior during design process, we need to remove current fluctuations due to transient evolution of the output voltage. We often do this by fixing the output voltage manually to a certain level (i.e. Vout ) when inspecting the charge pump output current. By doing this, we can observe charge pump's "pure" output current with respect to a certain output voltage level. Then, by performing sweep analysis with respect to Vout, we can obtain the charge pump current curve shown in the figure. This design trick mimics the worst possible condition for the charge pump where \(C_{LOAD}\) is so large that the output voltage does not change despite the pumping operation. Since the output voltage does not increase, maximum amount of charge is transferred from \(C_{p}\) to \(V_{OUT}\) node until \(V_{MID}=V_{OUT}\). In other words, under this condition, the total transferred charge is at its maximum, denoted by \( \Delta Q_{LOAD-MAX}=-\Delta Q_{MID-MAX} \) With this result, we can derive further \(I_{OUT-AVG-MAX}\) quantity which represents theoretical maximum output current of the charge pump as follows: \[ \Delta Q_{MID-MAX}=C_{p}(V_{OUT}-V_{DD})-C_{p}V_{DD}\] \[ \Delta Q_{MID-MAX}=C_{p}(V_{OUT}-2V_{DD})\] \[ \Downarrow \] \[ I_{OUT-AVG-MAX}=\frac{\Delta Q_{LOAD-MAX}}{T_{CLK}}=\frac{-\Delta Q_{MID-MAX}}{T_{CLK}} \] \[ I_{OUT-AVG-MAX}=\frac{C_{p}(2V_{DD}-V_{OUT})}{T_{CLK}} \]

Another important observation that we can make here is that currently, charge is only transferred to load during CLK=HIGH period and there is no current flowing to the load curing CLK=LOW period. To improve the uniformity of average output current further, we can simply connect two charge pump groups with opposite clock phases in parallel as shown in Figure 2 below.

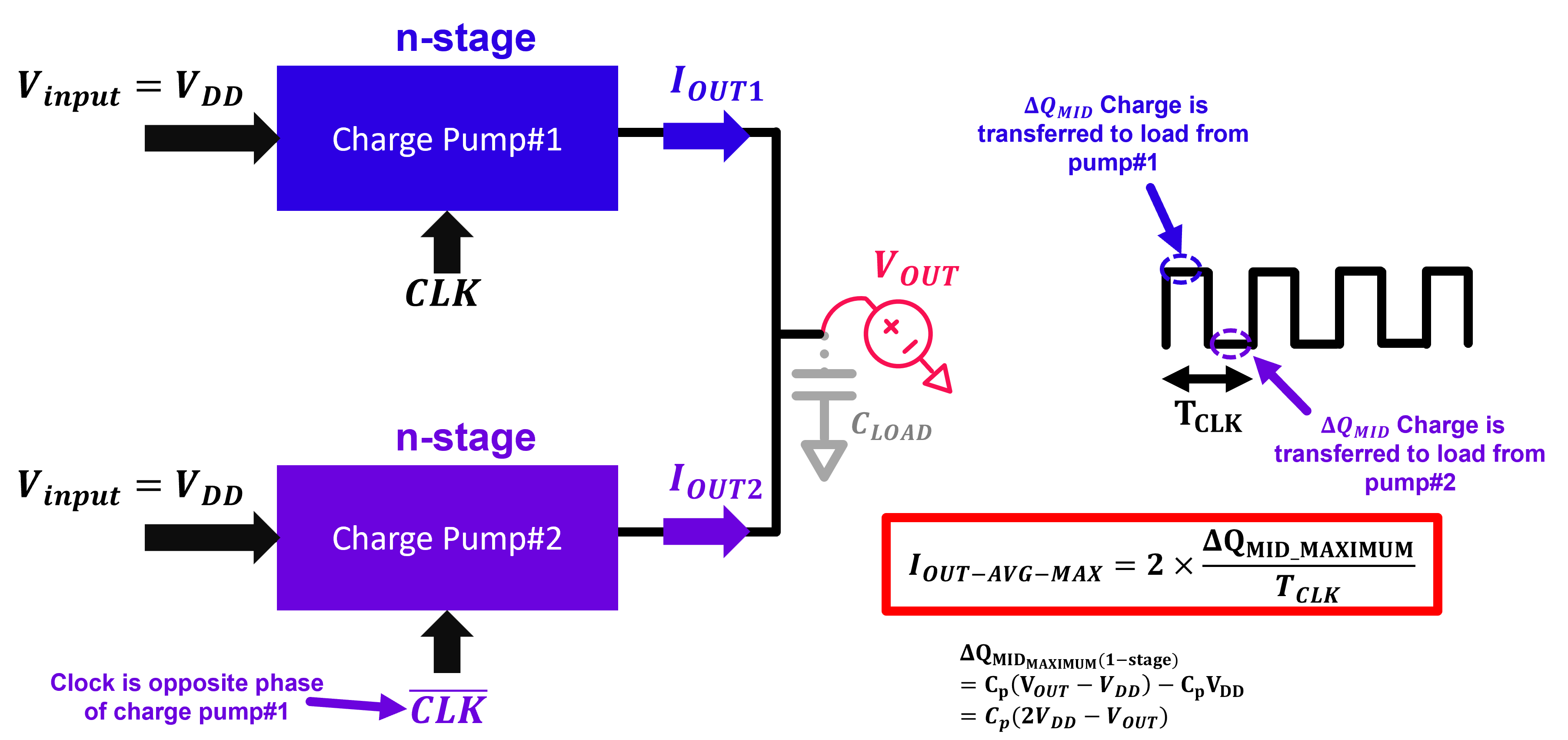
With this configuration, the two charge pump groups complement each other in providing current to the load. During CLK=HIGH period, current is provided to the load by charge pump#1, and charge pump#2 performs precharge operation. On the other hand, during CLK=LOW period, while charge pump#1 is performing prehcarge operation, current is provided to the load by charge pump #2. The maximum average output current of this charge pump structure can be expressed by the equations below: \[ I_{OUT-AVG-MAX}=\frac{2\Delta Q_{LOAD-MAX}}{T_{CLK}}=\frac{-2\Delta Q_{MID-MAX}}{T_{CLK}} \] \[ I_{OUT-AVG-MAX}=2\frac{C_{p}(2V_{DD}-V_{OUT})}{T_{CLK}} \]

One might argue that this structure does not improve pump performance since the doubled average output current is achieved at the cost of doubling the pump area and the same effect can be realized by simply doubling the pump capacitance without connecting more pumps in parallel. From average output current value point of view, this is indeed true. However, the parallel structure comes with added benefit of reduced pump's output voltage "ripple" since the charge transfers are distributed over the whole clock period. Therefore, the parallel structure is often preferable in real implementations than simply doubling the pump capacitance. It should be mentioned however that it is indeed a trade-off relationship. If the area overhead caused by added transistors are too large, it might be more beneficial to simply double the pump capacitance, achieving double the average current at the cost of increased "ripple" in the output voltage.