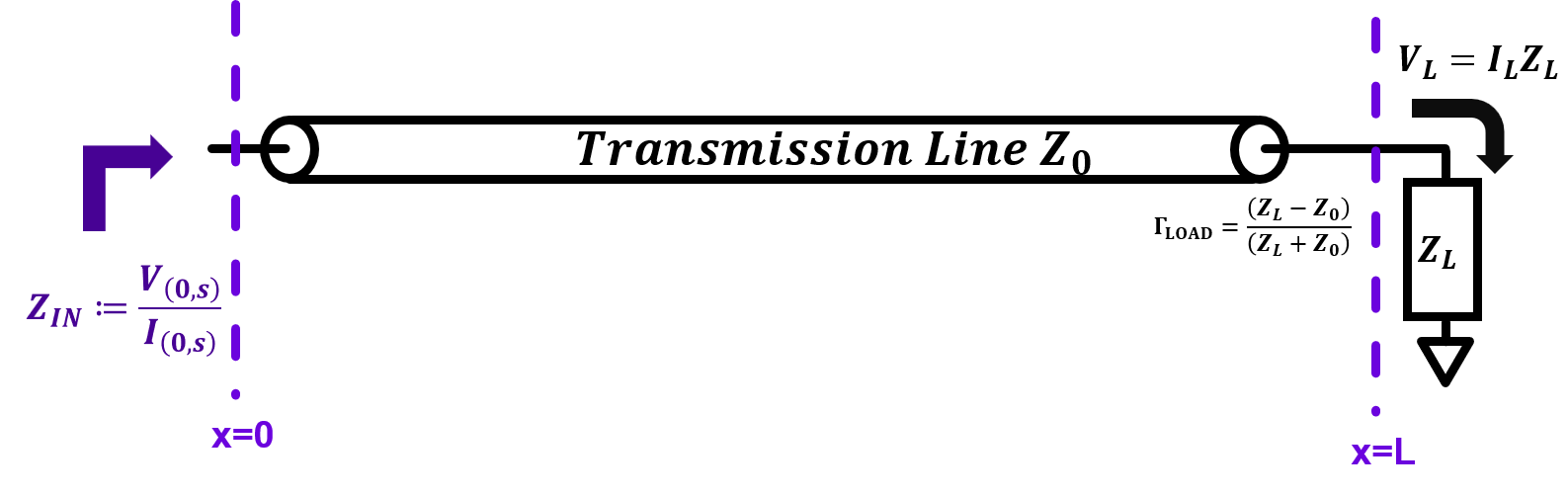
When we have a terminated transmission line as shown in Figure 1 above, we can define its input impedance as \(Z_{IN}=\frac{V_{(0,s)}}{I_{(0,s)}}\). This quanitity shows what kind of load the transmission line is perceived as by the components before it.

Before we derive the input impedance expression in detail, first let us recall voltage and current solutions for our example above which have been explained in previous chapters
( considering \(Z_{s}=0\) ): \[V_{(x,s)}=E_{(s)} \times \left[ \frac{1}{1+e^{-2s\sqrt{LC}\ell}\space\Gamma_{LOAD}}e^{-s\sqrt{LC}x}+\frac{e^{-2s\sqrt{LC}\ell}\space\Gamma_{LOAD}}{1+e^{-2s\sqrt{LC}\ell}\space\Gamma_{LOAD}}e^{s\sqrt{LC}x} \right] \] \[I_{(x,s)}=\frac{E_{(s)}}{Z_{0}} \times \left[ \frac{1}{1+e^{-2s\sqrt{LC}\ell}\space\Gamma_{LOAD}}e^{-s\sqrt{LC}x}+\frac{e^{-2s\sqrt{LC}\ell}\space\Gamma_{LOAD}}{1+e^{-2s\sqrt{LC}\ell}\space\Gamma_{LOAD}}e^{s\sqrt{LC}x} \right] \]

From the equations above, we can derive our input impedance expression by simply calculating the quantity \(Z_{IN}=\frac{V_{(0,s)}}{I_{(0,s)}}\) as follows: \[Z_{IN}:=\frac{V_{(0,s)}}{I_{(0,s)}}\] \[\Rightarrow Z_{IN}=Z_{0}\times \frac{1+e^{-2s\sqrt{LC}\ell} \space \Gamma_{LOAD}}{1-e^{-2s\sqrt{LC}\ell} \space \Gamma_{LOAD}}\] \[\Rightarrow Z_{IN}=Z_{0}\times \frac{ Z_{L}e^{s\sqrt{LC}\ell}+Z_{0}e^{s\sqrt{LC}\ell}+Z_{L}e^{-s\sqrt{LC}\ell}-Z_{0}e^{-s\sqrt{LC}\ell} }{ Z_{L}e^{s\sqrt{LC}\ell}+Z_{0}e^{s\sqrt{LC}\ell}-Z_{L}e^{-s\sqrt{LC}\ell}+Z_{0}e^{-s\sqrt{LC}\ell} } = Z_{0}\times \frac{ Z_{L}+Z_{0}\left( \frac{e^{s\sqrt{LC}\ell}-e^{-s\sqrt{LC}\ell}}{e^{s\sqrt{LC}\ell}+e^{-s\sqrt{LC}\ell}} \right) }{ Z_{0}+Z_{L}\left( \frac{e^{s\sqrt{LC}\ell}-e^{-s\sqrt{LC}\ell}}{e^{s\sqrt{LC}\ell}+e^{-s\sqrt{LC}\ell}} \right) } \] \[\Rightarrow Z_{IN}=Z_{0}\times \frac{ Z_{L}+Z_{0}\tanh(s\sqrt{LC}\ell) } { Z_{0}+Z_{L}\tanh(s\sqrt{LC}\ell) } \] While this equation might look underwhelming and does not give us any new insight as is, an interesting behavior emerges when we consider its operation under harmonic steady state condition (i.e. its frequency response). To derive the expression under harmonic steady state condition, we simply have to replace our laplace variable,\(s\) with \(j\omega\) in our equations. Here, \(\omega\) represents angular frequency of the harmonic steady state. By doing that, we obtain the following expression: \[ s \rightarrow j\omega \] \[\Rightarrow Z_{IN}=Z_{0}\times \frac{ Z_{L}+jZ_{0}\tan(\omega\sqrt{LC}\ell) } { Z_{0}+jZ_{L}\tan(\omega\sqrt{LC}\ell) } \] The equation in harmonic steady state above shows us a very interesting property of the input impedance. It shows us that the value of the input impedance of terminated transmission line is dependent on the angular frequency of interest, \(\omega\) . This means that the transmission line will behave differently depending on the signal frequency that goes through it.

Terminated transmission line, like our example is often called a "stub". Depending on the value of \(Z_{L}\), there are two special cases of such stubs which are often used in many applications, such as impedance matching.

• Short Stub ( \(Z_{L} = 0\) )
  When the end of a transmission line is shorted to ground, one might intuitively think that there will be no signal propagating in the transmission line since its voltage is shorted to ground. However, this is not true. Even in this case, due to reflection phenomenon in transmission line, there will be waves propagating and the TL's input impendance will be non-zero. To calculate the input impedance in this case, we can simply substitute \(Z_{L} = 0\) to the equation above which will yield us the result below: \[Z_{L} = 0\] \[\Rightarrow Z_{IN_{SHORTSTUB}}=Z_{0}\times j\tan(\omega\sqrt{LC}\ell)\] From this result, we can say that the input impedance of a short-stub can be considered equivalent to an inductor . Of course we should remember that the inductance value in this case can be positive or negative depending on the term \(\tan(\omega\sqrt{LC}\ell)\). Hence, a short stub can behave as either inductive or capacitive load depending on the signal's frequency and the transmission line's length.
  
  One common beginner mistake when using short-stub ( for example during impedance matching to a transistor) is connecting it directly to a transistor gate. We should remember that the impedance of a short-stub is only non-zero for \(\omega \neq 0\). Under DC condition (\(\omega = 0\)), the input impedance of the short stub will be zero, hence in this case the transistor's gate DC operating point will be zero if we connect the short stub directly to the transistor's gate ( most often this is not what the designer intended to do ). To use short-stub for impedance matching, we usually place a DC-block (i.e. large capacitor) between the short-stub and the transistor gate such that the transistor gate can be biased differently to the desired DC operating point.


• Open Stub ( \(Z_{L} \rightarrow \infty \) )
  When the end of a transmission line is open, one might intuitively think that signal propagating in the transmission line will always be equal to the input voltage since there is no load. However, this is also not true. Same as before, due to reflection phenomenon in transmission line, there will be non-zero load to the TL which is shown by the input impedance. To calculate the input impedance for open stub, we can simply approximate \( Z_{L} \rightarrow \infty\) which will yield us the equation below: \[Z_{L} \rightarrow \infty \] \[\Rightarrow Z_{IN_{OPENSTUB}}=Z_{0}\times \frac{1}{j\tan(\omega\sqrt{LC}\ell)}\] From this result, we can say that the input impedance of an open-stub can be considered equivalent to a capacitor . Of course, same as before, we should remember that the capacitance value in this case can be positive or negative depending on the term \(\tan(\omega\sqrt{LC}\ell)\). Hence open stub can behave as inductive or capacitive load depending on the signal's frequency and the transmission line's length.
  
  Unlike short-stub, we don't necessarily need to place any DC block between open stub and transistor gate if we want to use it for impedance matching to a transistor. This is because Under DC condition (\(\omega = 0\)) the input impedance of an open stub will be infinity. However when using open stub, one must make sure that the load condition at the end of the open stub is approximately close to "open". This is somewhat challenging in high frequency IC applications since parasitic capacitances might alter the load condition of an open stub.