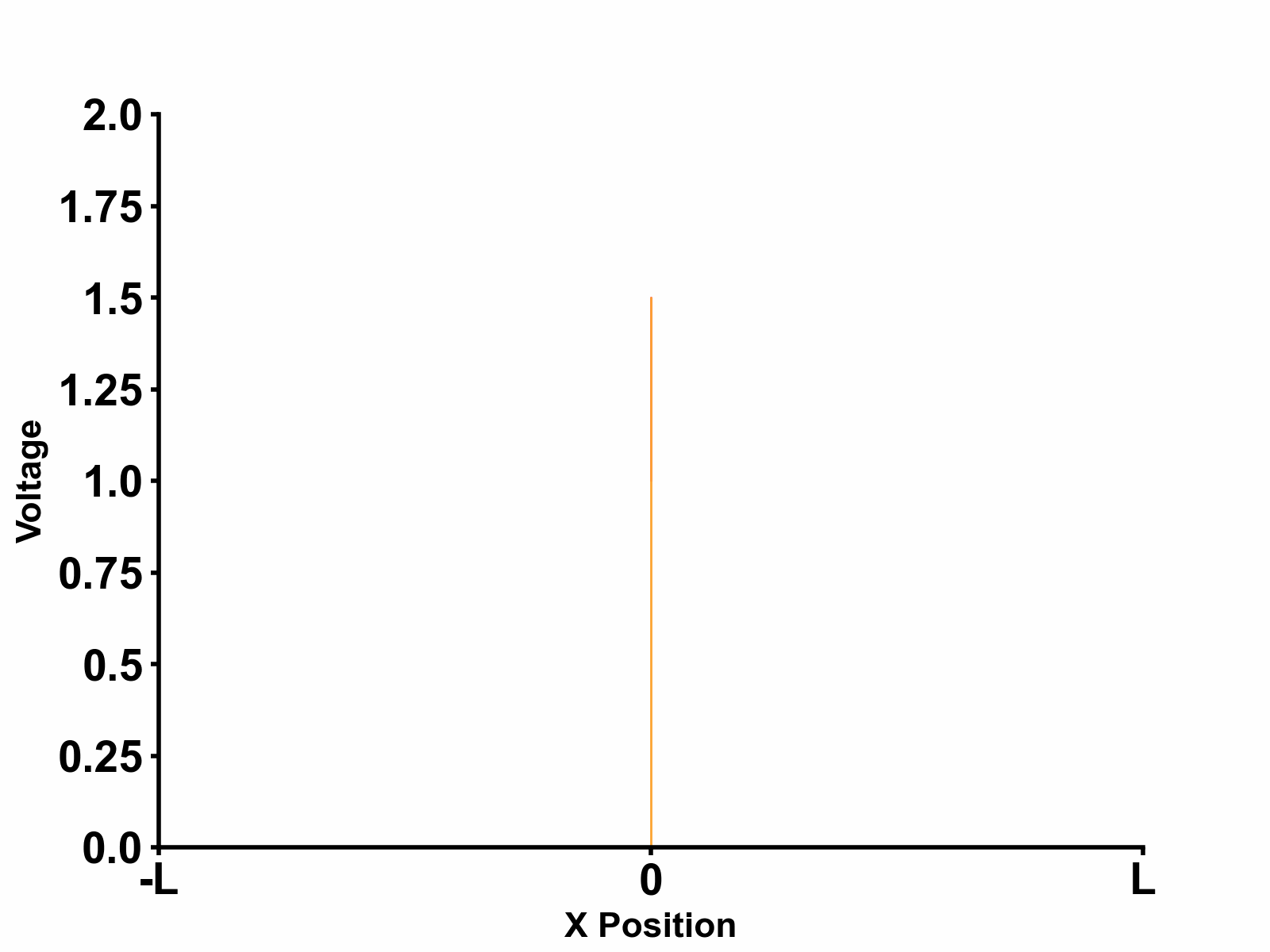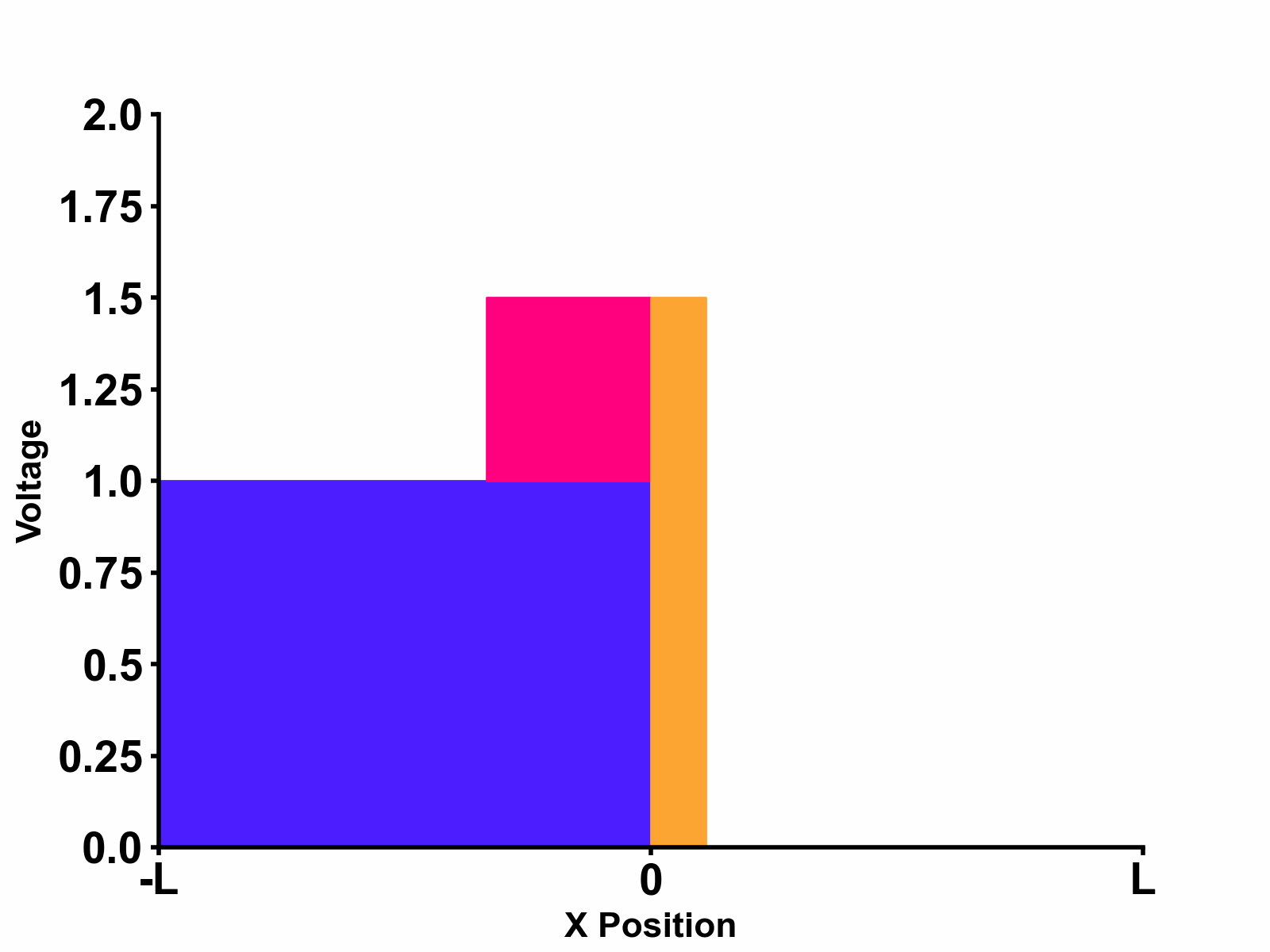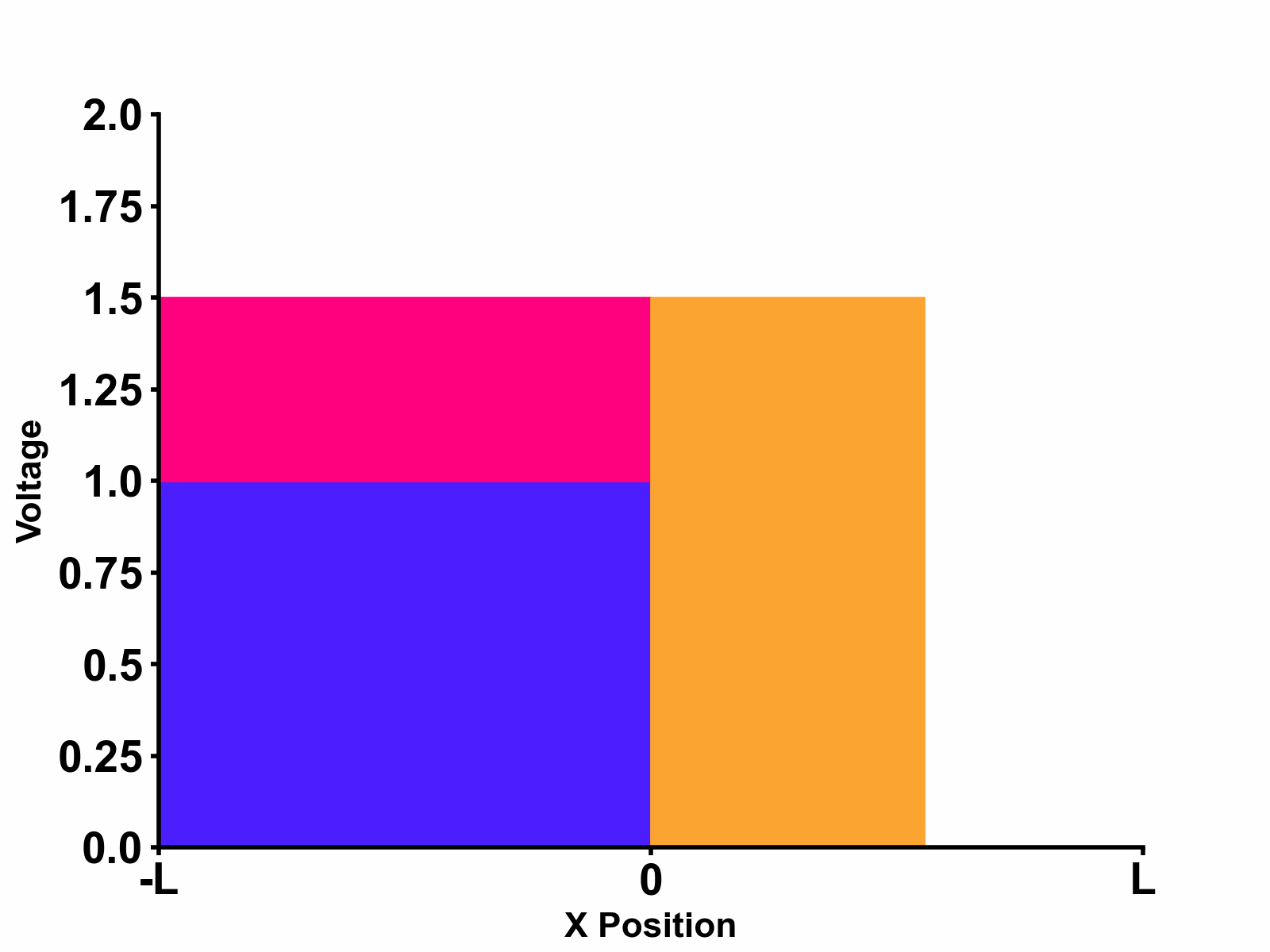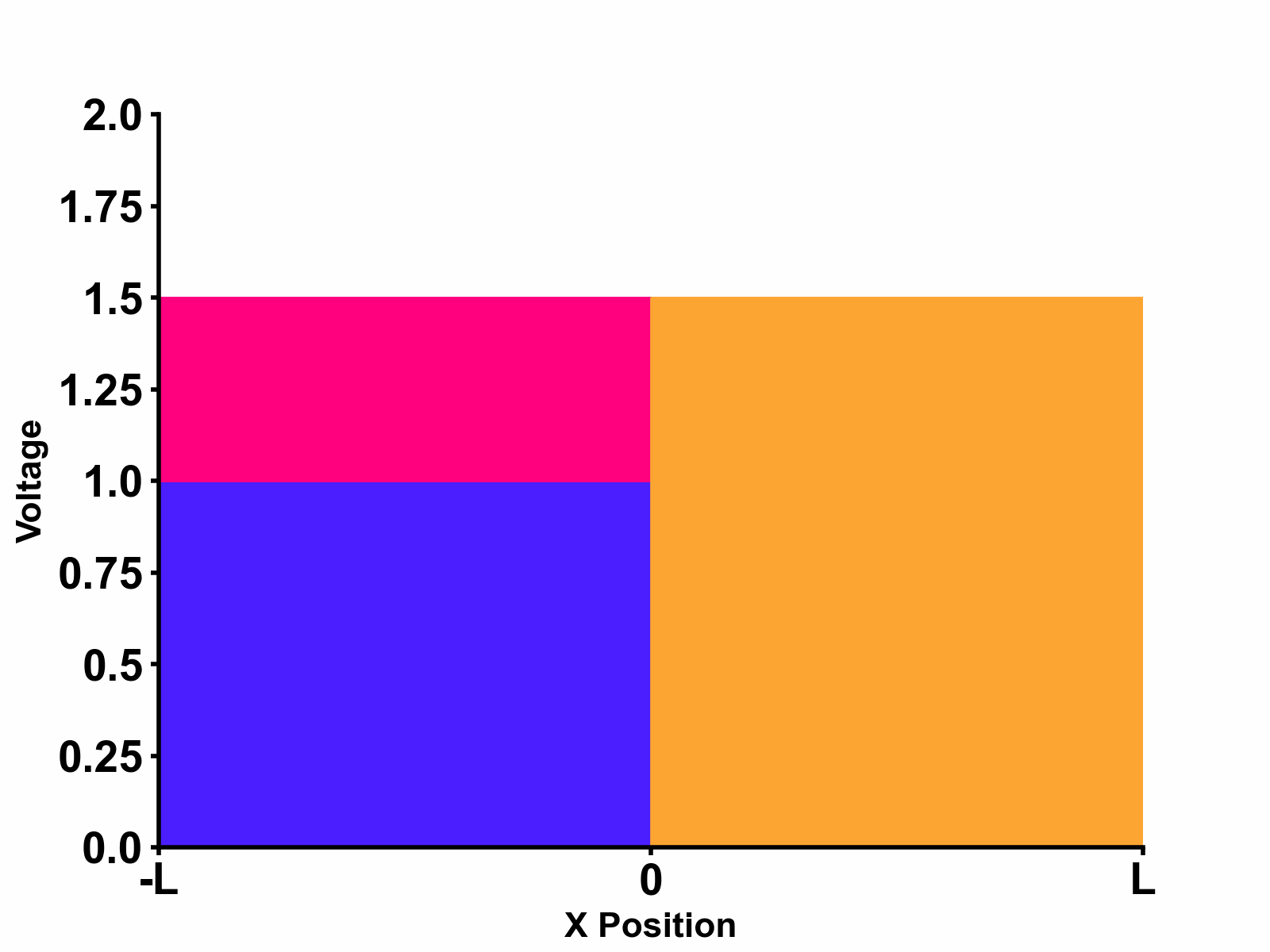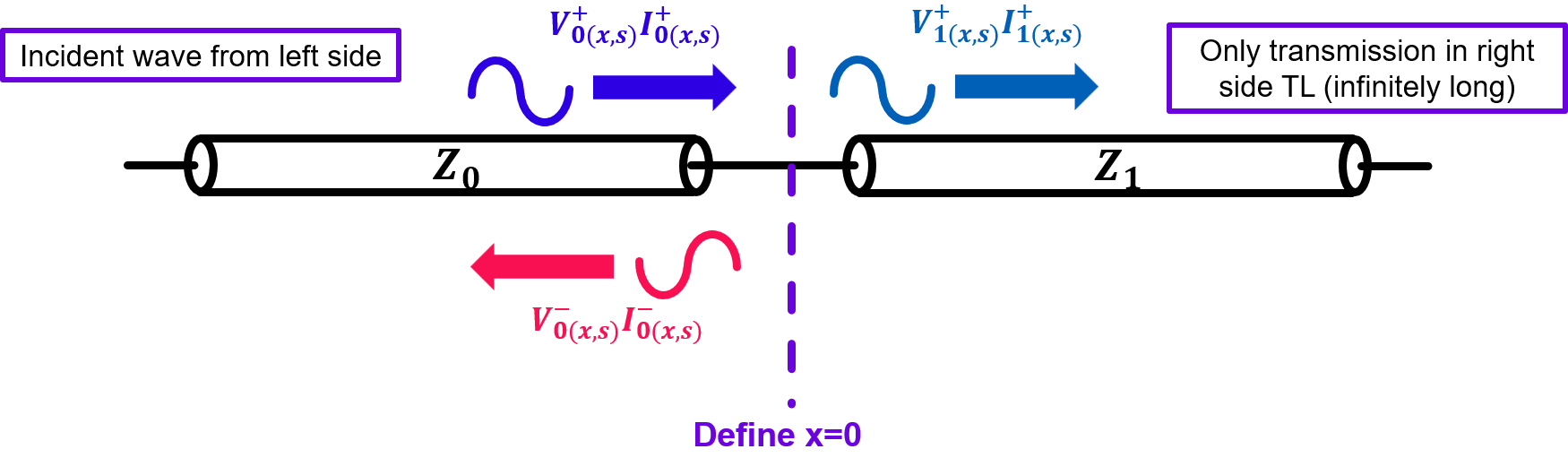
When a wave in a transmission line reaches a boundary to another medium, some energy is reflected and some is transmitted. Figure 1 above shows an example of such circumstances. In the example above, there are two different transmission line mediums with different characteristic impedances, \(Z_{0}\) and \(Z_{1}\). An incident wave propagating from left to right will first travel in medium \(Z_{0}\). The wave will then see the boundary between medium \(Z_{0}\) and \(Z_{1}\). As this happens, some of the wave's energy is transmitted to the second medium,\(Z_{1}\) while the rest is reflected back to the the first medium, \(Z_{0}\).

To derive the solution for our example above, let us define x=0 at the boundary and calculate the boundary conditions below:

• voltage continuity at boundary: \[V_{0(0,s)}=V_{1(0,s)}\] \[ \Rightarrow (V_{0+}+V_{0-})=V_{1+}\]


• current continuity at boundary: \[I_{0(0,s)}=I_{1(0,s)}\] \[ \Rightarrow \frac{V_{0+}}{Z_{0}}-\frac{V_{0-}}{Z_{0}}=\frac{V_{1+}}{Z_{1}}\] \[ \Rightarrow \frac{Z_{0}}{Z_{1}} \times \left( V_{0+}-V_{0-} \right)=V_{1+}\]

By substituting both equations, we can obtain reflection coefficient and transmision coefficient at boundary as follows: \[ Reflection \space coefficient \space \Gamma := \frac{V_{0-}}{V_{0+}}=\frac{Z_{1}-Z_{0}}{Z_{1}+Z_{0}} \] \[ Transmission \space coefficient \space T\space := \frac{V_{1+}}{V_{0+}}=1+\Gamma \]

From this we can express our final voltage and current solution as follows:

• Medium \(Z_{0}\) : \[V_{0(x,s)}=V_{0+}e^{-s\sqrt{L_{0}C_{0}}x}+\Gamma V_{0+}e^{s\sqrt{L_{0}C_{0}}x}\] \[I_{0(x,s)}=\frac{1}{Z_{0}}\times \left[ V_{0+}e^{-s\sqrt{L_{0}C_{0}}x}-\Gamma V_{0+}e^{s\sqrt{L_{0}C_{0}}x}\right] \]
• Medium \(Z_{1}\) : \[V_{1(x,s)}=TV_{1+}e^{-s\sqrt{L_{1}C_{1}}x}\] \[I_{1(x,s)}=\frac{1}{Z_{1}}\times TV_{1+}e^{-s\sqrt{L_{1}C_{1}}x} \]
We can see that that the wave propagation speed is different between medium \(Z_{0}\) and \(Z_{1}\) due to their different characteristic impedances. A more intuitive animation that shows the reflection and transmission at boundary between two different mediums is shown in the figure below.