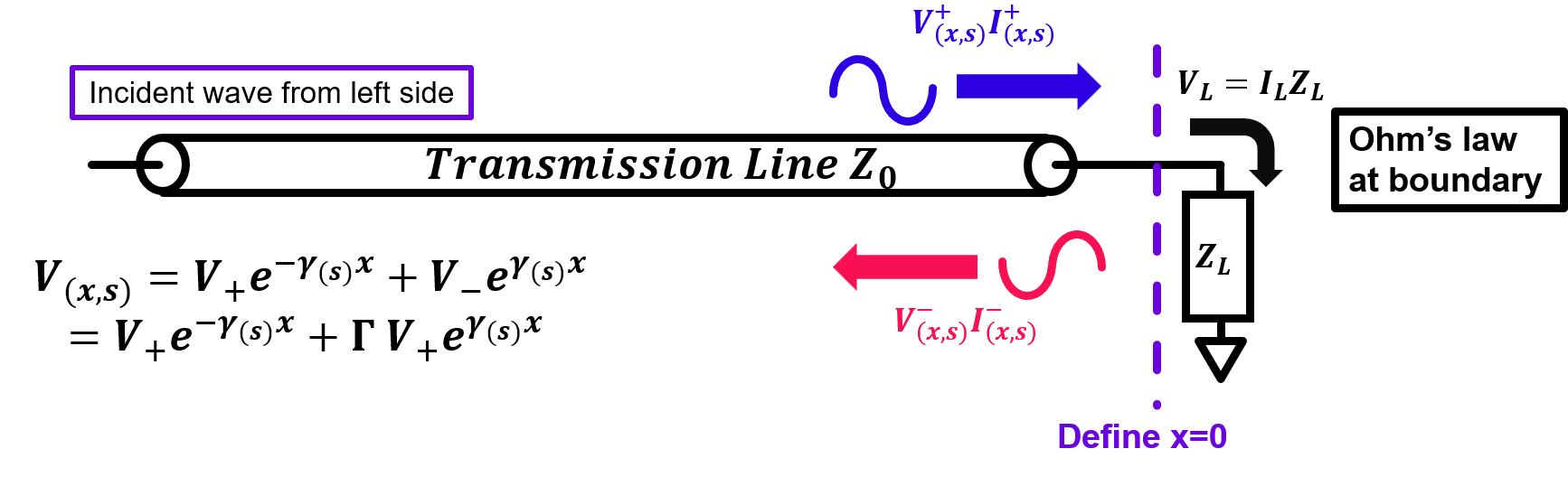
Realistically speaking, a transmission line cannot go on forever and must be terminated at some point. When this happens, there is bound to be reflection from the termination point. In this article we will explore how to analyze reflections in transmission line.

To easily derive the equations for reflection in terminated transmission line, there are three key concepts that we should keep in mind:

• Position \(x=0\) can be chosen arbitrarily (we will define x=0 at the boundary to simplify our calculations)
• Voltage and current are continuous at boundaries of different mediums (termination point in this case)
• Ohm's law can be applied at the termination load

Now let us calculate the boundary conditions that apply to our example above at \(x=0\) :

• Voltage boundary condition:\[V_{(0,s)}=V_{L}\] \[ \Rightarrow V_{+}e^{-s\sqrt{LC}0}+V_{-}e^{s\sqrt{LC}0}=V_{L}\] \[ \Rightarrow V_{+}+V_{-}=V_{L}\]
• Current boundary condition:\[I_{(0,s)}=I_{L}\]\[ \Rightarrow \frac{V_{+}}{Z_{0}}e^{-s\sqrt{LC}0}-\frac{V_{-}}{Z_{0}}e^{s\sqrt{LC}0}=\frac{V_{L}}{Z_{L}}\]\[ \Rightarrow \frac{Z_{L}}{Z_{0}}(V_{+}-V_{-})=V_{L}\]

Substituting both boundary conditions above, we get reflection coefficient ( \(\Gamma\) ) defined below: \[\Gamma:=\frac{V_{-}}{V_{+}}=\frac{Z_{L}-Z_{0}}{Z_{L}+Z_{0}}\] From this, we can obtain the final solution in laplace domain as follows: \[V_{(x,s)}=V_{+}e^{-s\sqrt{LC}x}+\Gamma V_{+}e^{s\sqrt{LC}x} \] \[I_{(x,s)}=\frac{V_{+}}{Z_{0}}e^{-s\sqrt{LC}x}-\frac{\Gamma V_{+}}{Z_{0}}e^{s\sqrt{LC}x} \] Step response for the circuit is shown in Figure 2 below. We can see that the incident wave is reflected in proportion to the reflection coefficient \(\Gamma\) which we derived.

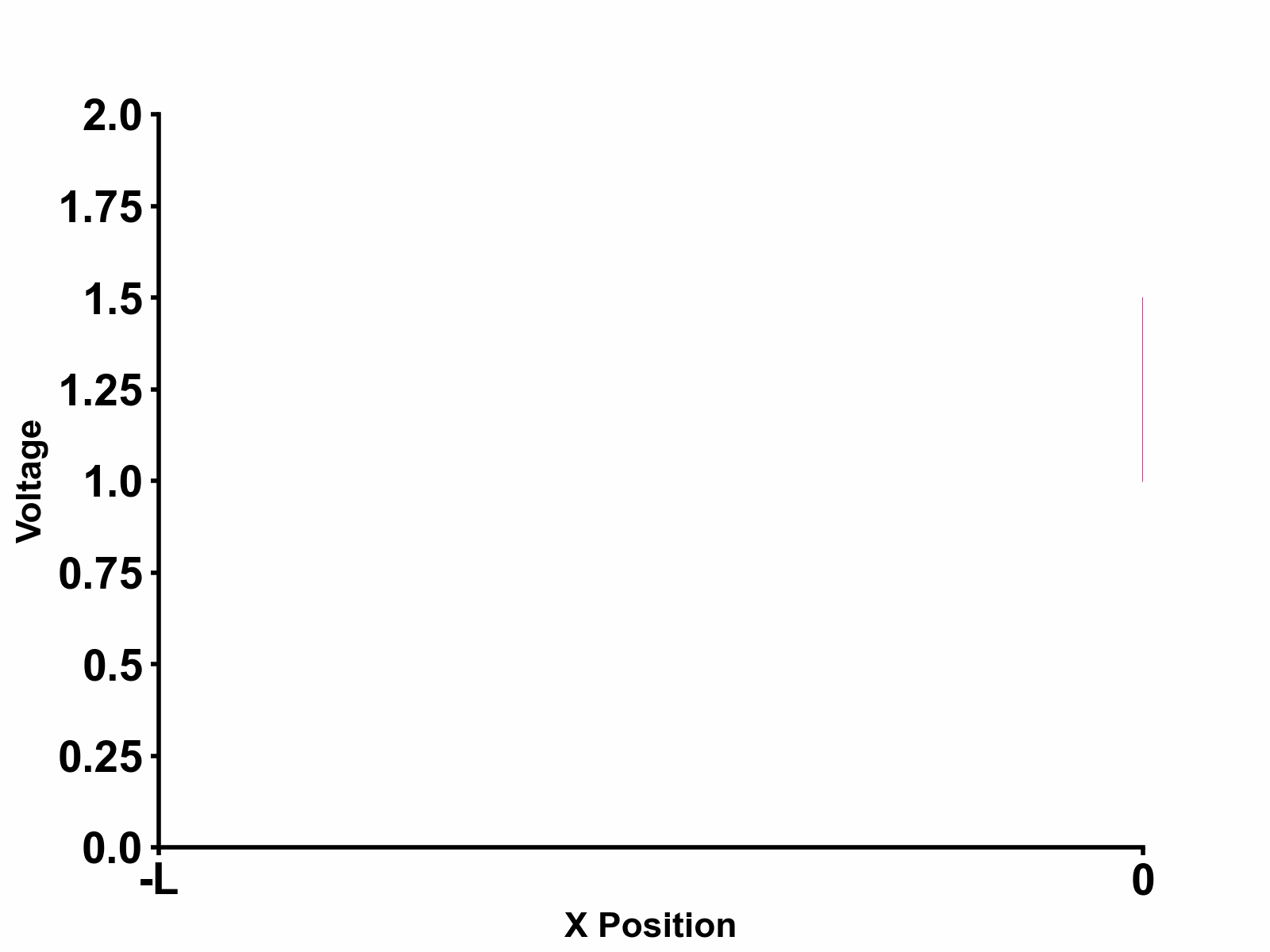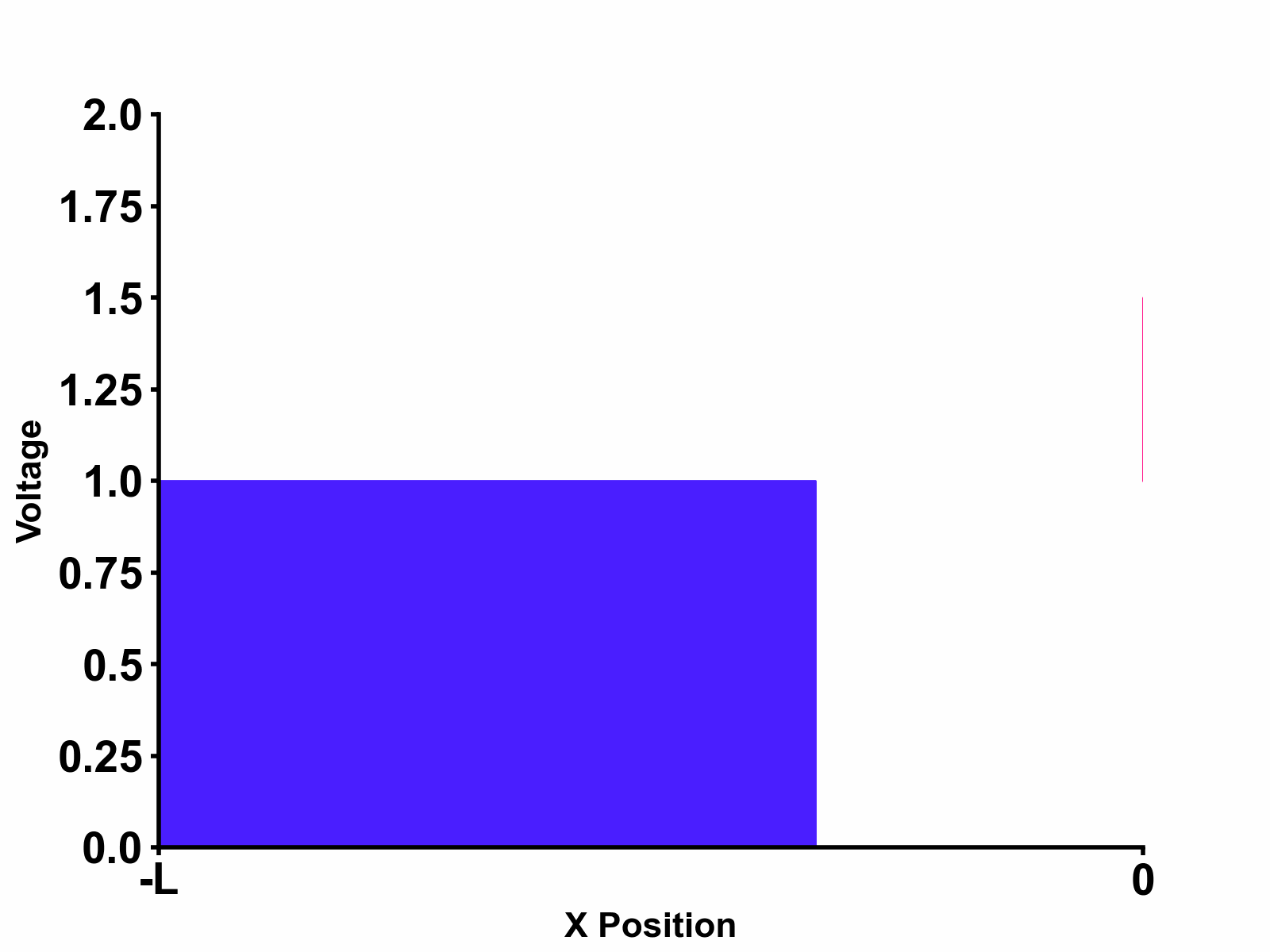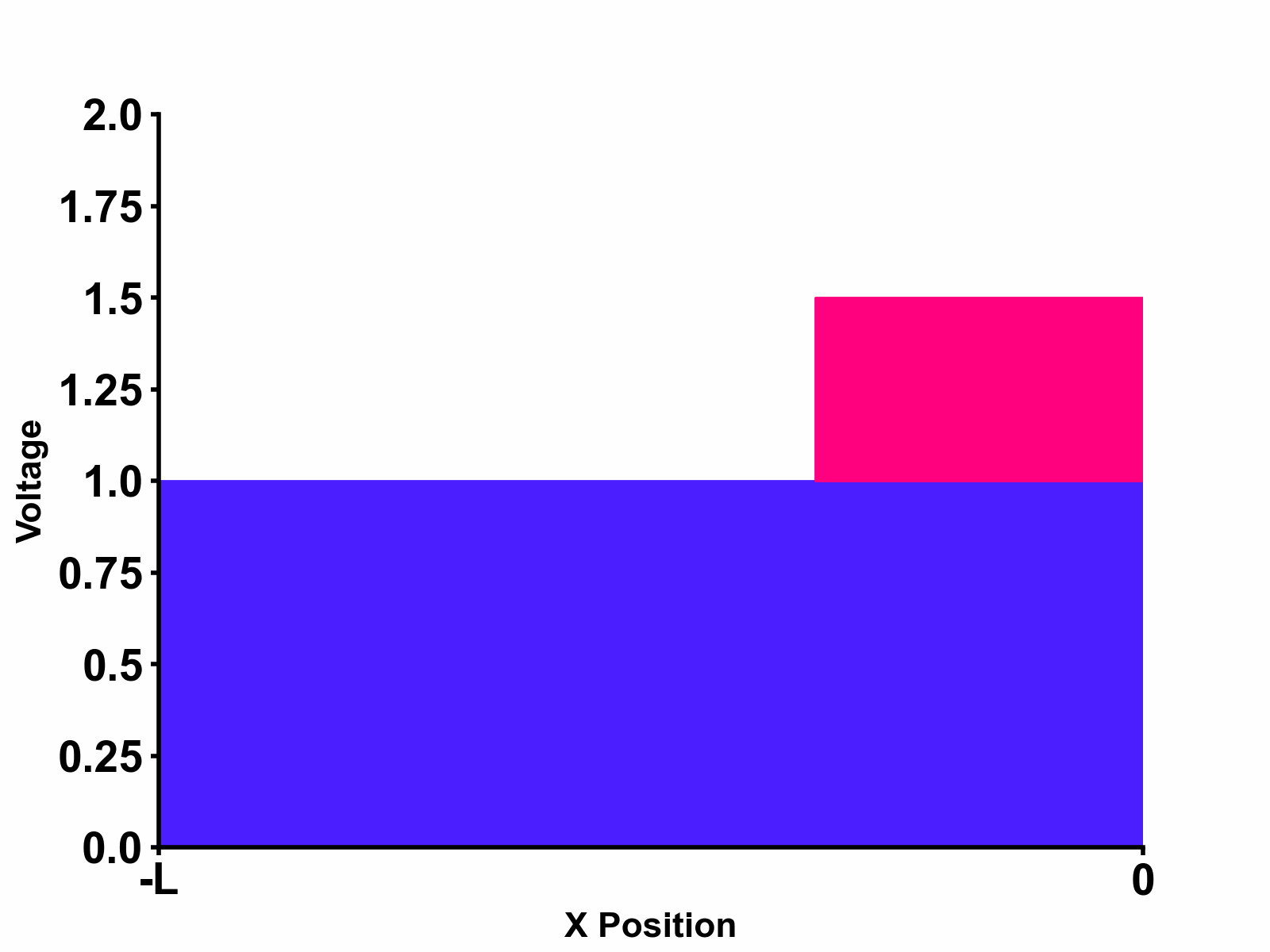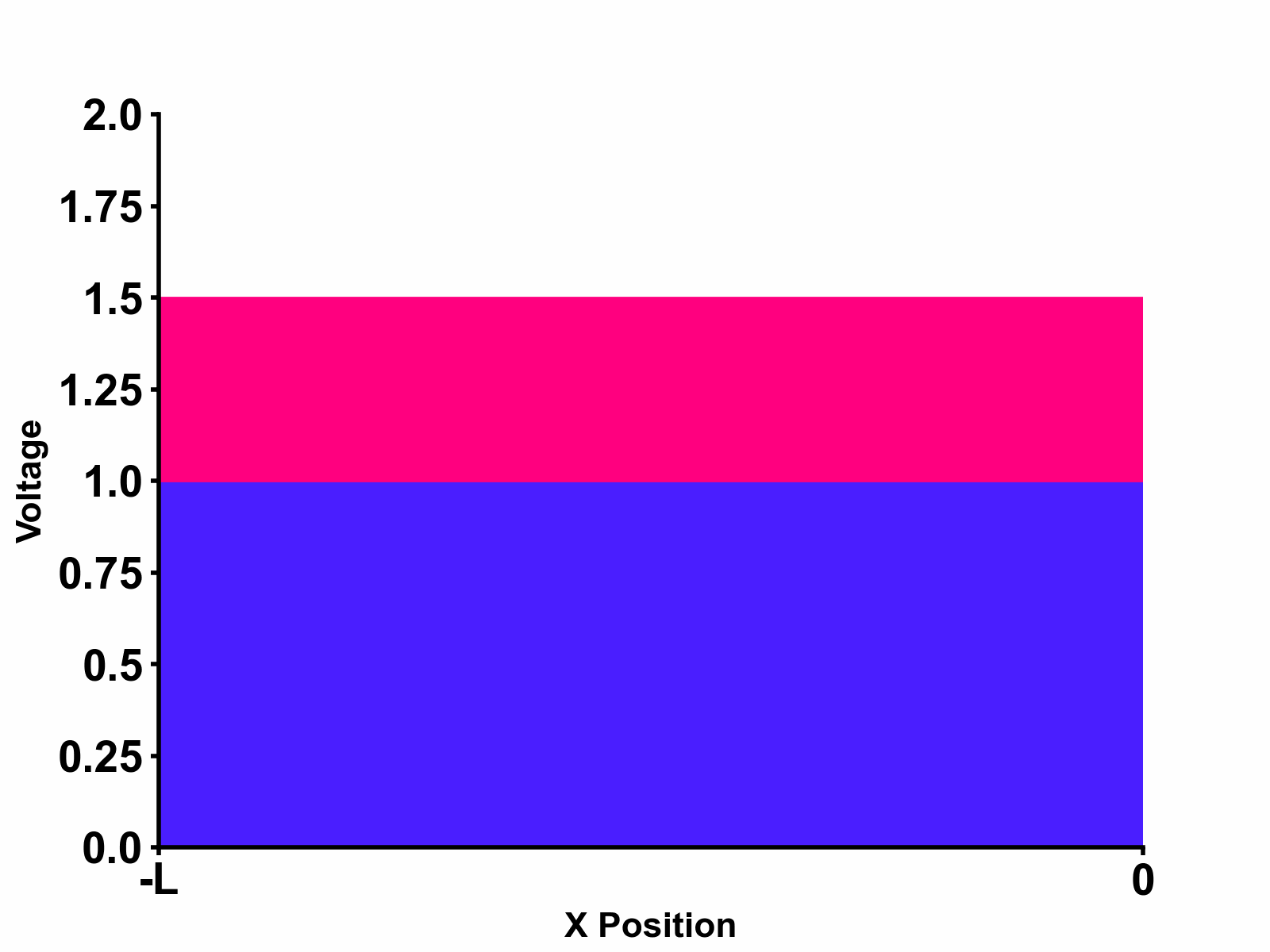
PS: While defining x=0 at boundary is useful for gaining intuition on the reflection phenomenon at the boundary, we should remember that the reflection only occurs when the wave has "propagated" and reached the said boundary. This means that there is usually a time delay before the reflection wave appears due to limited propagation speed in transmission line. Furthermore, the reflected wave will also need some time before it reaches the observed point of interest. This means that the reflection coefficient \(\Gamma\) is actually \(\Gamma(x,s)\) since the observed delay is dependent on location x and where we define x=0. While things can get complicated, we should always keep in mind that the difference in equation is just mathematical artifact and they still describe the same physical phenomenon. In the next chapter, we will explore an example which will showcase this point further.